It seems a straightforward question at first, but two people pondering this question could come to two different conclusions. According to Wikipedia, “A mountain is a large landform that stretches above the surrounding land in a limited area, usually in the form of a peak....There is no universally accepted definition of a mountain.” If we try to define a mountain as rising above a certain altitude, a problem arises. What prevents a boulder jutting out from the ground of a high mountain from being a mountain itself? It seems rather obvious that this boulder is just a part of the larger mountain. In an opposite case, consider Mt. Adams of the Presidential Range. Mt. Adams is New Hampshire’s second highest mountain, but why is it not deemed ‘just a part of the larger mountain’ (Mt. Washington) just like the boulder in the first example? It seems so much larger somehow, but what makes it so?
There is no way to define a mountain, but there is a way of measuring how much of a mountain a mountain is. This is called prominence. Prominence is the vertical distance between a mountain’s summit and its key col, which is the lowest point on the highest ridge connecting the mountain to a higher place. In simpler terms, if you are standing on a mountain, its prominence is the minimum vertical distance you must descend to reach a higher place. If the prominence of your mountain is 500 feet, you must drop at least 500 feet, no matter which direction you walk in, before you can begin to climb to an elevation higher than its summit.
If the concept of prominence seems confusing, this 2D diagram may help you understand it. Mountain B is called the line parent of Mountain A.
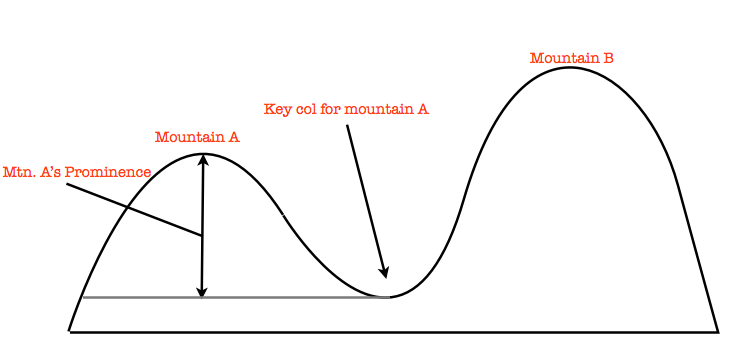
Most hiking lists, like the 4000-footers, use a prominence cutoff, like 200 feet, to determine which mountains may be on the list. Now, if the simple definition you just heard satisfies you, you may leave this page and return to what you were doing. But if you wish to learn more about prominence and the logic behind it, read on! Caution: some sections may be technical and difficult to understand.
Notice that if you were to climb down a different side of the mountain, you might be able to descend a much greater distance before encountering a higher mountain. This slope of the mountain could descend to a plain which stretches for miles without any mountains at all. Someone standing in this plain may perceive the mountain as being “massive, dominant, and impressive”, when there is actually a much greater and more prominent mountain behind it. Look to New Hampshire’s Presidential Range for an example. The northeast slopes of Mt. Madison drop 4,000 feet down into the lowlands around Gorham and the Androscoggin River, but it only has 466 feet of topographic prominence. Why? Because on its southeast side, it is separated from taller Mt. Adams by a col at elevation 4900’. If you are standing on Mt. Madison and want to climb Mt. Adams, you must descend a minimum of 466 feet. This is how much Mt. Madison “stands out” from the Presidential ridgeline.
Obviously, you could create other routes which may descend further from the summit, but they would all have to leave the ridge top connecting the two mountains. This is because the key col is not just a low point; it’s a high point as well. It is a low point in an obvious way, since it is clear where the lowest spot on the ridgetop is, but it may not be clear how a col is a high point. In fact, every point on a ridge is a high point! If you were to look straight up a ridge, pick a random point, and draw its outline from your perspective, ignoring everything above that point, then you would draw a 2D mountain. The summit of your mountain marks the ridgetop. This should not be hard to understand, since this is just the definition of what a ridge is: the high ground. The key col is special because it is both the high point just like every other point on the ridgetop, and the low point of the ridge.
Some ridges are very obvious, such as those that lead from lowlands to mountaintops, while others connect minor peaks to larger mountains and may be very indistinct. Even what many people may perceive as simply “hillsides” or “slopes” have ridges, even if they are the most minor rises. Everywhere there is a peak, there is a ridge - even a boulder jutting out of the ground, like the one mentioned at the beginning of this article, would theoretically have a “ridge” connecting it to a higher place. Obviously, the only ridges that we care about are the ones that are easily visible.
Ridges are important because they connect peaks. You may define a ridge as connecting only two peaks, or you could view one long chain of ridge-connected peaks as one long ridge, such as the Southern Presidentials or the Franconia Ridge. All ridges may be considered part of other ridges, even the most major ones, all the way up to a landmass’s primary ridge. For example, the ridge connecting Mt. Lincoln to Mt. Lafayette is a small, simple ridge, but from there, a major ridge leads to Mt. Washington. And an even more major (though very indistinct in places) ridge connects Mt. Washington to the higher Appalachian Mountains to the south. Remember, when we say this is a "major" ridge, it is because it is the highest route across a vast area. It is not necessarily noticeable in the sense that the terrain is rugged. You could continue this process all the way up to Aconcagua, highest mountain in the Americas. You may end up following the same section of ridge back and forth, depending on which peak you start with. You will cross many cols along the ridge, but by definition of prominence, you must cross the key cols of Lincoln, Lafayette, Washington, and so on. So we see that there are many different ways to think of ridges, but the most basic way to break them up is to say that they connect one peak to another - in between any two peaks, you will find exactly one ridge, with exactly one lowest point. This shows that every col is a key col for only one mountain, and every mountain has only one key col.
Ridges may merge as they climb to a peak, just like converging waterways. This is because rivers and streams always follow drainages - the exact opposite of ridges. Imagine a huge, circular valley - all sides of the valley lead down to one low point at the bottom of the valley. Water will clearly always collect at the bottom of the valley since it’s just like a giant bowl. Just as streams join and become rivers before they empty into the ocean, our valley will likely have many small brooks that join and become larger as they flow toward the bottom. All of these brooks will end at the lowest point in the valley, which will, inevitably, become flooded as time progresses, but let’s ignore that for now.
This valley has now become a “negative” of a mountain. This means that if the valley were to be filled with plaster, the cast would be a mountain. The low point represents the summit, while all of the waterways represent the mountain’s ridges. Notice that even the original valley has ridges, too - they are found between the brooks. When the cast is taken, these would become drainages. This further illustrates that ridges and drainages are opposites.
Now, we have showed that a basic ridge connects two peaks, but clearly a ridgeline must begin somewhere other than a mountain, since ridges lead to mountains in the first place. Every drainage is bounded by two ridges: this is very logical since between any two high places, there is naturally a lowest place where water can flow. By the same logic, every ridge is also bounded by two drainages. If you are walking down on a ridge from a mountain, there are two drainages on each side of you. Since drainages always merge as they flow toward the ocean, just like ridges always merge as they “flow” toward the summit of a mountain, the two brooks on each side of you will eventually join and that is where your ridge will end. Thus, if you continue following the top of a ridge down from your mountain, you will eventually end up at a place where two waterways join together.
So we know that ridges begin at the convergence of two drainages and “flow” uphill to the summit of a mountain and connect mountains. We also know that drainages flow downhill and end at the ocean. But where do drainages begin? Drainages begin on opposite sides of a ridge. This is because of a super-easy-to-understand property of water - it always flows downhill! If water falls a ridgetop, it will never flow straight down the ridge; it must diverge to one side or the other. Because a col is the lowest point on the ridgetop, this makes it a very likely location for two drainages to begin. In other words, because a col is a low point, water naturally collects there, but because it is also a high point, water can never stay there (although if the area around a col is very flat, there will likely be some sort of pond).
You will often find the source of two major rivers in the drainages on either side of a major col. For example, the key col for Mt. Lafayette, highest mountain in a fairly large region, is Crawford Notch, and the Saco River begins at Saco Lake, just to the south of Crawford Notch. (Note - Crawford Notch is usually used to describe the entire region walled in by Mt. Webster and the Willey Range, but the actual col is somewhere near the Crawford Depot, at the “Gateway Region”). This is not always the case, for extremely isolated mountains almost always have their key col in a very flat location where it is nearly impossible to identify any sort of ridge. Mt. Washington’s key col is in the middle of the Champlain Canal in New York. This appears to contradict what was said earlier - that a ridge cannot cross a waterway. However, remember that since canals are man-made, they are not drainages. Water can flow both ways through them.
The smaller a mountain’s prominence, the more obvious the location of the key col is. For mountains with a prominence less than 2000 feet, you can find it by hand using a topographical map using the method described here. Cases of mountains any more prominent than that are best left to a computer, so you should not pick a mountain which is the highest in a large region. Note: It is helpful to follow this procedure on a topographic map while reading this section. First, pick a random elevation contour near the mountain you choose. It is helpful to pick a bolded contour line because it will be easier to see. You may need a magnifying glass. Next, follow that line with your finger until you arrive back at the point where you started. Now, if your finger went completely around your mountain without also encircling a higher one, then the key col is at a lower elevation than that contour. If you did encircle a higher mountain while following the line, then the key col is higher. Now, choose another elevation contour that is either higher or lower than the first, depending on what you found on the first trial. Repeat the procedure until you have found the two contours which are on opposite sides of the key col. Remember, this means that one contour will encircle your mountain without going around any higher mountains, while the one directly below it will encircle both your mountain and at least one higher mountain. Now, take the average of the elevations of these two contours. The result will be the approximate elevation of the key col. Finally, to find the mountain’s prominence, subtract this value from the elevation of the summit. If the summit elevation is not given on the map, estimate it by adding half the elevation contour interval to the elevation of the highest contour on the mountain. Once you know this information, finding the location of the key col is easy, since you have already deduced which two contours it is between. Because one contour encircles a higher mountain and one does not, they will break off from each other at some point and rejoin at the same place. This area is the general location of the key col. If you fully understand the concept of prominence and the ridgeline of the key col, this should make sense.
This diagram may help if it doesn’t. The green lines are the contours (viewed from the side) which encircle only mountain A, while the red lines are the contours which encircle mountain A and also its line parent, mountain B. If the lines represent 100-foot contours, mountain A’s prominence is 797 feet (remember, we’re estimating the elevation of the key col).
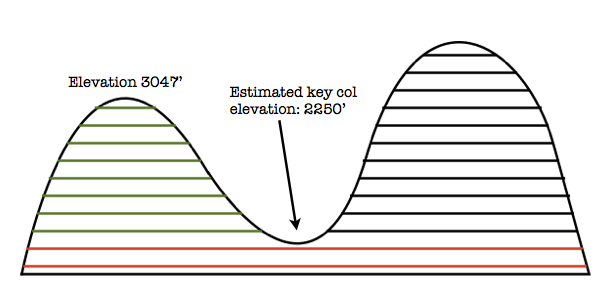
The prominence we calculated with this method is called average prominence. There are two other commonly used methods of calculating prominence. Clean prominence uses the lowest possible elevation for the summit (if it is not given) and the highest possible elevation for the key col to produce the minimum prominence value. Optimistic prominence uses the highest possible elevation for the summit and the lowest possible elevation for the key col to produce the maximum prominence value. Of these three methods, average prominence has the greatest chance of being more accurate than the other two.
There is one special case of a mountain which cannot follow the rules of prominence. This is the highest mountain on a landmass. Since higher mountains are only found across the ocean, the key col is considered to be at sea level. The prominence of these special case mountains is equal to their elevation. The same applies for Mt. Everest, even though there are no higher mountains across the ocean. Some topographers prefer to use what is known as dry prominence, which ignores water and uses the terrain on the ocean floor to calculate prominence.
Recall from earlier in this article that a mountain’s line parent is the first higher mountain encountered while following the ridge across the key col. You may have noticed that this brings up the question which began this article, “What is a mountain?”. It turns out that the line parent depends on how many mountains you are willing to consider as mountains. Topographers will usually use a prominence cutoff when finding the line parent. To avoid this opinion-based system, the parent mountain can be defined in another way, by adding one condition to the definition of the line parent: that the parent mountain is also more prominent than its child. This is called the prominence parent. The prominence parent may be the same as the line parent, but if it is not, all you must do to find it is continue up the ridge from the line parent. For example, if you are calculating the prominence of Mt. Eisenhower, the first higher peak you will encounter while following the highest ridge leading to higher terrain is Mt. Franklin. Although Mt. Franklin is higher than Mt. Eisenhower, it is hardly more than a tiny knob on the ridge. If you continue the process by following the highest ridge to higher ground from Mt. Franklin, the next peak you will come to is Mt. Monroe. Mt. Monroe is more of a mountain than Mt. Franklin; it’s included on the 4000-footer list. But its 264 feet of prominence is still less than Eisenhower’s 335. If you continue up the highest ridge to higher ground from Mt. Monroe, you will finally reach Mt. Washington. Mt. Washington is then the prominence parent of Mt. Eisenhower.
There is a third type of parent, called the island parent and also known as the encirclement parent. This parent, defined much differently than the other two, is the highest mountain in the area encircled by the elevation contour just below the key col. To understand this confusing definition, imagine there is a worldwide flood, and the oceans rises to the White Mountains. We’re going to think about the island parent of Mt. Flume. Because the White Mountains are higher than the areas around them, they would eventually become an island. Let’s imagine the water continues to rise and all the major mountain ranges of the White Mountains become islands. The Franconia Range becomes one such island and Mts. Lafayette, Lincoln, Liberty and Flume are all on one island together, and they are separated from all other mountains by the ocean. If the ocean rises above the key col of Mt. Flume, Mt. Flume then becomes its own, separate island, while Mts. Lafayette, Lincoln, and Liberty are still on an island together. However, if the ocean stops just short of the key col, all the peaks remain on the same island, and the key col becomes a narrow isthmus. Since Mt. Lafayette is the highest point on this hypothetical island, it is the island parent of Mt. Flume (it is also the island parent of Mt. Liberty and Mt. Lincoln). It is interesting to note that if a mountain has a key col lower than that of the highest mountain in a large region, than the island parent for the first mountain will be very far away. This usually occurs with small hills near the ocean, which can have an island parent in another country or even continent. This should make sense, since if the key col elevation is only a few hundred feet above sea level, the hypothetical island will have the same general shape as the landmass the mountain is on.
A concept related to prominence is isolation. Isolation is defined as the distance (usually in miles) between a mountain’s summit and the nearest higher land. This higher point is called the isolation limit point. You might think that the isolation limit point will be on the slope of the line parent, but this is not necessarily true. A mountain (mountain C) may be connected to its line parent (mountain D) by a very long and gently sloping ridge, while a ridge with a very sharp and deep col connects it to another higher mountain (mountain E). Mountain C’s isolation limit point is therefore on the side of mountain E, because it is closer to mountain C than mountain D (mountain C’s parent) is. (See diagram below)
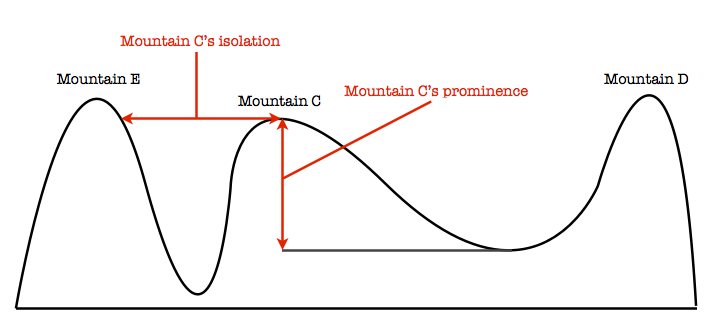
The closest higher mountain to any given mountain is called the nearest higher neighbor (NHN). A mountain’s isolation limit point is usually on the slopes of its NHN.
Unlike with prominence, island high points are not a special case, although their isolations will always be very high, since you would have to cross the ocean to get to higher mountains. Mt. Everest’s isolation is undefined. That brings us to the end of this article about prominence. We hope we’ve given you a new perspective of mountains and that you will explore this interesting topic further.